Physics 101 - Homework # 7 Solutions

Note: Symbols written in Bold are vectors.

Chapter 9

Problem 8)

a) = (33.33 rev/min)(2 rad/rev)(1 min/60 s) = 3.490 rad/s down (away from the viewer)
b) From the definition of average acceleration, we have
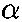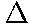
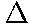av = / t
= [0 -3.49 rad/s]/(4.791 s)
= -0.7285 rad/s2;   the negative sign means that the direction is up (toward the viewer)

Problem 19)

The constant tension will cause a constant acceleration; we can solve for the acceleration using our knowledge of the motion:
x = x0 + v0t + (1/2)at2
0.8 m = 0 + 0 + (1/2)a(1.5 s)2
a = 0.71 m/s2
The final speed of the string can then be found using
v = v0 + at = 0 + (0.71 m/s2)(1.5 s) = 1.07 m/s
This is the speed of a point on the rim of the spool; thus the final angular speed is
= v/R = (1.07 m/s)/(1 x 10-2 m) = 107 rad/s
The work done by the tension as the string unwinds produces the kinetic energy of the spool:
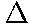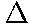W = Fx = K = (1/2)If2 - (1/2)Ii2
(20 N)(0.8 m) = (1/2)I(107 rad/s)2 - 0
which gives
I = 2.8 x 10-3 kgm2
Alternatively, one can use 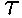= I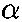, where the torque is FR, and the angular acceleration can be found using
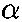= (1/2)t2

Problem 20)

The rotational inertia of the dumbell about the center is
I1 = m(½L)2 + m(½L)2 = m½L2
The rotational kinetic energy is
K1 = ½I12
= ½[½(2.5 kg)(0.80 m)2][(400 rev/min)(2 rad/rev)/(60 s/min)]2 = 7.02 x 102 J
The rotational intertia of the dumbell about the end is
I2 = 0 + mL2 = mL2
The rotational kinetic energy is
K2 = ½I22
= ½[(2.5 kg)(0.80 m)2][(400 rev/min)(2 rad/rev)/(60 s/min)]2 = 1.40 x 103 J

Problem 37)

We will need to find out what torque is required to loosen the bolt, i.e. we must solve problem 36 first. The force supplied by the plumber is just equal to his force of gravity (weight), thus the torque can be found from
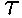= rFsin = (0.45 m)(74 kg)(9.8 m/s2)sin90° = 3.26 x 102 Nm
He needs to exert this same torque, but now with a moment arm given by (0.45 m)sin50°, so we have
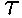= rFsin
3.26 x 102 Nm = (0.45 m)m(9.8 m/s2)sin50°
which gives
m = 96.6 kg

Problem 38)

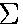
We find the angular acceleration from 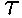= I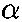, where we consider torques about the center of the flywheel:
FL = I
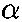
(-10.0 N)(0.30 m) = (25 kg-m2)
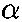
which gives
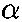= - 0.12 rad/s2
For the angular motion, we have
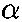= 0 - t
0 = (6.0 rad/s) + (-0.12 rad/s2)t
which gives
t = 50 s

Problem 48)

Let's choose the upward direction as positive. The identical tops have equal rotational inertia about their centers. Because the only torques acting on the tops are internal, angular momentum is conserved:
I1 + I2 = I3 + I4
If the slower top has the angular speed of 5 rad/s, we have
I(10 rad/s) + I(-12 rad/s) = I(5 rad/s) + I4
which gives
4 = -7 rad/s   downward
If the faster top has the angular speed of 5 rad/s, we have I(10 rad/s) + I(-12 rad/s) = I3 + I(-5 rad/s)
which gives
3 = +3 rad/s   upward

Problem 60)

The initial rotational kinetic energy is
Ki = ½I2
= ½(½MR2)2
(recall that I = ½MR2 for a cylinder about its symmetry axis)
= (1/4)(20 kg)(0.50 m)2[(300 rev/min)(2 rad/rev)/(60 s/min)]2
= 1.2 x 103 J = 1.23 kJ
Because the rotational speed does not change, the increase in the kinetic energy is the kinetic energy of the 0.2 kg mass. The speed of this mass is R, so its kinetic energy is
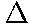Km = ½m(R)2 = K
The percentage change is
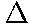(K/Ki)100 = [½m(R)2/½(½MR2)2]100
= 200 m/M = 200(0.2 kg)/(20 kg) = 2%

Chapter 10

Problem 17)

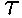= r x F
= (3i - j -5k   m) x (2i + 4j + 3k   N)
= (17i - 19 j + 14 k) N·m

Problem 18)

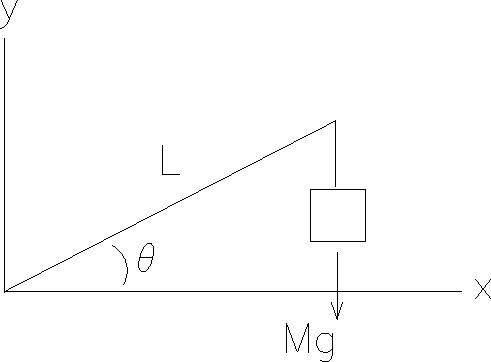
With the coordinate system as given in the diagram we can find the torque using
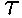= r x F
= Lcosi + LLsinj) x (-Mgj)
= -MgLcosk
= -(65 kg)(9.8 m/s2)(2.4 m)cos30° k
= -1.3 x 103k Nm
The direction of the torque is -k, i.e into the page.

Problem 24)

At a steady speed, dL/dt = 0, thus we must have a net torque of zero. There are two torques contributing, both of which are directed along the axle, with that due to F being outward, and that due to mg inward, which we'll take as the positive directiion for torques. Therefore we have
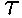net = 0
mgr1 - Fr2 = 0
which gives
F = mg(r1/r2)
= (200 kg)(9.8 m/s2)(10 cm)/(50 cm)
= 390 N

Problem 30)

The angular momentum of the skater is conserved (there is no net external torque):
L =I11 = I22
(Iskater + 2 mr12)1 = (Iskater + 2 mr22)2
2 = {(Iskater + 2 mr12)1}/( Iskater + 2 mr22)
= {(2.9 kg m2 + 2(5 kg)(0.9 m)2)(1 rev/s)}/( 2.9 kg m2 + 2(5 kg)(0.3 m)2))
2 = 2.89 rev/s

Problem 49)

We treat the child as a point mass moving on a radial line of the platform. For the system of child and platform, angular momentum is conserved:
L = Iplatform0 = (Iplatform + mchildR2)1
(450 kg m2)(0.8 rad/s) = [450 kg m2 + (32 kg)(2 m)2]1
which gives
1 = 0.623 rad/s
The change in energy
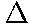K = ½(Iplatform + mchildR2)12 - ½Iplatform02
½[450 kg m2 + (32 kg)(2 m)2](0.62 rad/s)2 - ½(450 kg m2)(0.8 rad/s)2
= -33 J
The work was done by the force of friction between the child and the platform, which is necessary to enable the child to walk.

Physics 101 Solutions
Physics 101 Home page
Physics Department Home Page
College of William and Mary, Dept. of Physics

armd@physics.wm.edu
last updated: Sept 3 2000