Physics 101 - Homework # 9 Solutions

• Problem 13-3
• Problem 13-6
• Problem 13-31
• Problem 13-36
• Problem 13-47
• Problem 13-75
• Problem 13-78
• Problem 14-3
• Problem 14-7
• Problem 14-31
• Problem 14-43
• Problem 14-47
• Problem 14-52
• Problem 14-64

Chapter 13

Problem 3 )

The spring moves as an harmonic oscillator. The general expression for x is

x = Acos(t + )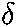

from which we get the velocity

v = dx/dt = - Asin(t + )

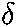We compare this with what we are given, v = 0.4sin(t + ) m/s, and we see that

A = 0.4 m/s

so

A = (0.4 m/s)/(2.00 rad/s) = 0.2 m

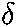since we are given =2.00 rad/s. Because sin(+) = -sin(), we can see that =0. Thus we have

x = 0.2 cos(t)

We obtain   a   by differentiating the velocity

a = dv/dt = 0.4cos(t + ) = - 0.8cos(t) m/s²

We now plot these functions:

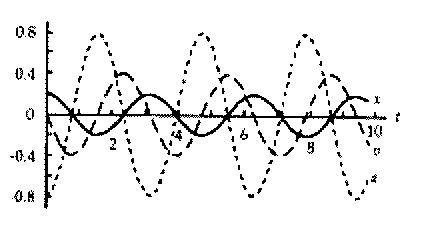
Problem 6 )

We have v_max = A and a_max = A², so we get

= a_max/v_max

= (1.66 m/s²/(0.486 m/s)

= 3.42 rad/s

The amplitude is A = v_max/ = (0.486 m/s)/(3.42 rad/s) = 0.142 m

Problem 31 )

We use a coordinate systm with up=positive. At the equilibrium position of the 25-g mass, we have

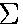F = k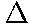y - mg = 0.

Thus

k = mg/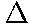y = (25 x 10^-3 kg)(9.8 m/s²)/(12 x 10^-2 m) = 2.04 N/m

For the 75-g mass, the angular frequency is

= (k/m)^1/2 = [(2.04 N/m)/(75 x 10^-3 kg)]^1/2 = 5.22 rad/s

Thus the period is

T = 2/ = 2/(5.2 rad/s) = 1.20 s

Problem 36 )

The angular frequency is

= 2/T = 2/(2.5 s) = 2.51 rad/s

Because the total energy is the maximum kinetic energy, we have

E = ½mv_max² = ½mA²²

2.7 J = ½(1.2 kg)A²(2.51 rad/s)²

which gives

A = 0.844 m

Problem 47 )

a) From   T = 2 (L/g)^1/2 for a simple pendulum

we get

L = gT²/4² = (9.8 m/s²)(3 s)²/4²

= 2.23 m

Because g depends on the distance from the center of the Earth,

  g = GM/r²

we can write

g₂/g₁ = (r₁/r₂)² = [R_e/(R_e+h)]²

or

g₁/g₂ = [1 + (h/R_e)]²

where   R_e   is the radius of the Earth and the height of the skyscraper is   h << R_e.

Since the length of the pendulum does not change, we get

T₂/T₁ = (g₁/g₂)^1/2 = 1 + (h/R_e)

Thus

(3.0002 s)/(3 s) = 1 + (h/R_e)

which gives

h/R_e = 6.66 x 10^-5

or

h = (6.66 x 10^-5)(6.37 x 10⁶) = 425 m

Problem 75 )

a) The natural frequency of the system is

₀ = (k/m)^1/2 = [86 N/m)/(0.548 kg)]^1/2 = 12.5 rad/s

From problem 74 we have that resonance occurs when have

² = ₀² - (b²/2m²) = (k/m) - (b²/2m²)

(12.2 rad/s)² = [(86 N/m)/(0.548 kg)] - [b²/2(0.548 kg)²)]

which gives

b = 2.20 N·s/m

The lifetime is 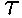  = m/b = (0.548 kg)/(2.2 N·s/m) = 0.25 s

The sharpness can be expressed as

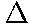
= 2b/m = 2(2.2 N·s/m)/(0.548 kg) = 8 rad/s,

or by using the Q-factor:

Q = ₀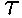 = (12.5 rad/s)(0.25 s) = 3.1

Problem 78 )

a) If we evaluate x = (0.5 m)sin(t + 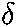) at time t=0, we get

-0.1 m = (0.5 m)sin(0 + ) which gives 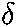= -0.20 rad or - 0.20 rad.

To choose between these two, we have to use v=dx/dt = (0.5 m)cos(t + 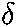). At t=0 s, we get

- 1 m/s = (0.5 m)cos(-0.20)

or = (0.5 m)cos( -0.20)

Because must be positive, we select the cosine that is negative: 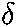= - 0.20 rad = 2.94 rad

b) From

- 1 m/s = (0.5 m)cos(-0.20)

we get = 2.0 rad/s, and thus

f = /2 = 0.32 Hz

c) we find the acceleration from a = dv/dt = - (0.5 m)²sin(t + ). At t=0 s, we get

a = -(0.5 m)(2.0 rad/s)²sin(0 + - 0.20 rad)

= + 0.42 m/s² (positive x-direction)

d) The total energy is E = (1/2)kA²;

5 J = (1.2)k(0.5 m)²

which yields k = 40 N/m

e) We can get the mass from m from ² = k/m:

m = k/² = (40 N/m)/(2.0 rad/s)² = 9.6 kg

Chapter 14

Problem 3 )

For the wavelength and the frequency we have

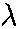= L/N   and   f = 1/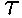

where 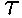is the period. We can get the tension using

f = (1/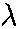)[T/µ]^1/2 = (N/L)[T/µ]^1/2

where N is the number of wavelengths, so

1/(0.10 s) = [3.5/(2.7 m)][T/(220 x 10^-3 kg/m)]^1/2

T = 13 N

Problem 7 )

Because the two strings have the same volume density, their linear densities are related by (recall that the area is the radius squared...)

µ₂/µ₁ = (R₂/R₁)² = (3)² = 9

Since the wavelengths are the same, the frequencies are in the ratio

f₂/f₁ = (T₂/µ₂)^1/2/ (T₁/µ₁)^1/2

= (T₂µ₁/T₂µ₁)^1/2

thus

T₁/T₂ = (f₂/f₁)²(µ₂/µ₂)

= (1/3)²(9) = 1

The tensions are the same.

Problem 31)

The speed of the wave is

v = (T/µ)^1/2

= [(800 N)/(12 g/cm)(10^-3 kg/g)(10² cm/m)]^1/2

The angular frequency is

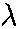= 2f = 2v/ = 2(26 m/s)/(0.7 m) = 230 rad/s

The average power is then

P_average = (1/2)µA²²v = (1/2)(1.2 kg/m)(5 x 10^-2 m)²(230 rad/s)² (26 m/s)

= 2.1 x 10³ W

Because the speed depends only on the medium, and thus does not change, we have

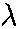' = 2v/' = 2v/2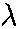 = (1/2)

Because there is no change in amplitude or speed we have

P_average' = (1/4)P_average = (1/4)(2.1 x 10³ W) = 5.3 x 10² W

Problem 43)

We find the intensity of the sound 5 m from the source using

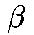= 10log₁₀(I/I₀)

83 dB = 10 log₁₀(I/10^-12 W/m²)

which gives

I = 2.0 x 10^-4 W/m²

The power output is the total rate at which the energy passes through a sphere:

P = IA = I(4r²)

= (2.0 x 10^-4 W/m²)4(5 m)² = 6.3 x 10^-2 W

Problem 47)

The wavelength from a stationary source travelling toward the observer is

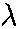= v/f_s = (330 m/s)/(160 Hz) = 2.06 m

This wavelength approaches the observer at a relative speed of v+v_O; thus he hears a frequency of

f = (v + v_O)/ 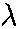= (330 m/s + 26 m/s)/(2.06 m) = 147 Hz

Problem 52)

a) Let's use the general Doppler shift equation

f = f₀[(v + v_o)/(v - v_s)]

Here the observer is at rest so   v_o = 0. Thus we have

f = (185 Hz)(330 m/s)/(330 m/s - 27 m/s) = 201 Hz

b) Your speed is (50 mi/h)(30 m/s)/(67 mi/h) = 22.5 m/s. Now we have a moving source and a moving observer. The source is moving away from the observer so there is a downward shift of frequency due to source motion, and the observer is moving towards the source so there is an upward shift of frequency, so the relevant signs are as given;

f = f₀[(v +v_o)/(v +v_s)]

= (185 Hz)[(330 m/s + 23 m/s)/(330 m/s + 27 m/s) = 183 Hz

Problem 64)

Since v = 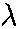f, we have

a) f = v/ 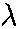= (245 m/s)/(2.5 m) = 98 Hz

b) A point of the string moves with simple harmonic motion with amplitude A = 0.14 m. The angular frequency of this motion is

= 2f = 2(98 Hz) = 616 rad/s

The maximum transverse velocity occurs at the midpoint of the motion with magnitude

v_max = A = (0.14 m)(616 rad/s) = 86 m/s

The maximum transverse acceleration of a point of the string occurs at the maximum deflection with magnitude

a_max = A² = (0.14 m)(616 rad/s)² = 5.3 x 10⁴ m/s²