Physics 101 - Final Exam 1994

Lecturer: H.C. von Baeyer

Problem 1

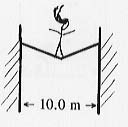
A circus performer, who weighs 500 N, walks across an unstretchable wire 10.1 m long strung between two rigid supports which are separated by 10 m. Assume that the wire is massless. When she reaches the halfway point, what is the tension in the wire?

Problem 2

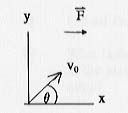
A 0.5 kg soccer ball is kicked from the ground with an initial speed of V₀ = 30 m/s at an angle of = 30°. It is pushed forward by a tail-wind with a steady force of F(Wind)=(5 i)N . Use g = 10 m/s².

1. Write down equations for V_x , V_y , x, and y as functions of t, using numerical values for the accelerations and initial velocities.
2. How long is the ball in the air before it hits the ground?
3. How far did it travel?
4. How far would it have travelled if the wind were in the opposite direction?

Problem 3

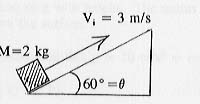
A 2 kg mass moves up a ramp with initial speed = 3 m/s. The ramp is inclined at 60° to the horizontal, and the coefficient of kinetic friction between the mass and the ramp is 0 (no friction).

1. List all the forces acting on the mass.
2. What is the work done by each force as the mass moves a distance x up the ramp?
3. How far up the ramp does the mass travel before coming (momentarily), to rest?
4. Repeat a), b), c) for the case where the coefficient of kinetic friction between the mass and the slope is 0.3, and the coefficient of static friction is 0.4.

Problem 4

A 0.01 kg bullet is fired into a 1.99 kg block. The block is attached to a spring (spring constant 500 N/m) and the block (containing the bullet) slides without friction to the right, compressing the spring by 0.4 m. What was the speed of the bullet v₀?

Problem 5

An object is projected upward from the surface of the earth with an initial speed of 4 km/s.

1. Find the maximum height it reaches above the surface of the earth. Neglect air resistance, but take into account the variation of g with height. The radius of the earth is about 6000 km and g = 10 m/s² on the surface.
2. Compute the maximum height under the assumption that g = 10 m/s² = constant.
3. Explain the sign of the difference between  a) and  b).

Problem 6

A wheel with a heavy rim of mass M and radius R is suspended from a string of length h attached to its handle of P. The distance between the origin at the center of the wheel, and the point P, is d. The wheel rotates as shown with angular velocity .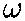

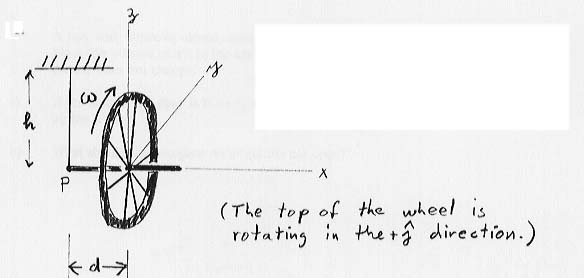
1. Write an expression for the angular momentum L of the wheel, in terms of M, R, d, h, 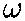, and the unit vectors i, j, k.
2. Write an expression for the torque on the wheel about the point P, using the same variables.
3. If the wheel is released in the position shown, in which direction will its center begin to precess? Use unit vector notation, and justify your answer (No credit for guessing.)

Problem 7

A car, with windows closed, misses a turn and sinks into a lake to a depth of 4 m. Since the volume of air in the car does not change as the car sinks, the air pressure in the car does not change.

1. If the area of the door is 0.5 m², what is the force exerted on the outside of the door by the water?
2. What should the occupant do to get the car open?

Problem 8

A harmonic wave on a string is described by y(x,t) = 0.2 sin (30 x + 20 t) where x and y are in meters and t in seconds. Find

1. The speed and direction of the wave
2. The wavelength
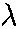
3. The frequency f
4. The period T
5. The maximum displacement
6. By using v_y = dy/dt, find the maximum transverse speed of a particle of string