A 4 kg mass is attached to a spring which has a spring constant of 16 N/m. The spring is stretched to 5.0 cm from the equilibrium position, and released (starting with zero initial velocity). Assume there is no friction or damping. For the resulting oscillation, find the:

a) amplitude

b) period

c) maximum speed of the mass

d) magnitude of the maximum acceleration of the mass

e) position of the mass after 2 seconds

f) the general equation of motion, i.e. x(t)

A very similar example was done in lecture, and problem 13-15 from the homework is also very similar. It is an example of simple harmonic motion (SHM).

a) By definition of the amplitude, it is 5.0 cm (or 0.05 m).

b) 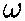= [k/m]^1/2 = [(16 N/m)/(4kg)]^1/2 = 2 rad/s

T = 2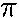/ 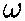= 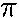seconds

c) The general equation for SHM is

x(t) = A cos( 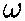t + )

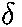so can get the speed from

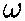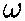dx/dt = -A sin ( t + )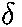

and thus the maximum speed is

v_max = A

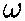
= (0.05 m)(2 rad/s) = 0.10 m/s

d) Similarly, the maximum acceleration is

a_max = A 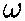²

= (0.05 m)(2 rad/s)² = 0.20 m/s²

e) We have x = A cos( 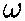t + 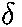), where here 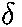=0, since the function is at its maximum at time t=0 (starting at rest, with maximum stretch). Plugging in   t = 2s,   we have

x(t=2s) = (0.05 m) cos [(2 rad/s)(2 s)] = -0.033 m

f) The general equation of motion is

x = (0.05m) cos[(2 rad/s)t]