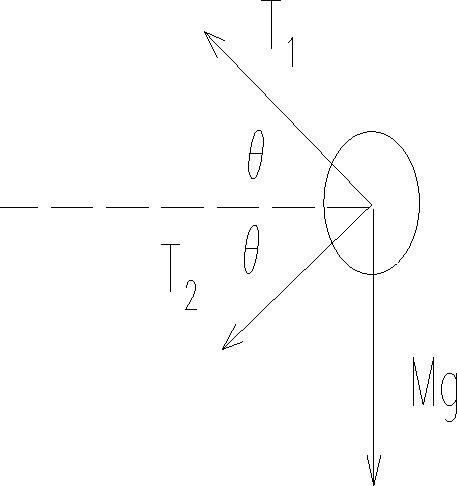
Problem 4:
A mass (M = 5 kg) is attached to a vertical axis
by two light (i.e. massless) strings as shown.
Each string has a length of 0.6 m, and the angle
 = 30° .
If the system is rotated about the axis with frequency
of 3 revolutions per second, what are the tensions in the
two strings? (hint: they are not the same!)
= 30° .
If the system is rotated about the axis with frequency
of 3 revolutions per second, what are the tensions in the
two strings? (hint: they are not the same!)
Solution:
Choose a coordinate system with y=positive upwards and x=positive towards
the center of the rotation, i.e. towards the axis.
Draw a force diagram for the mass and apply F = Ma:
-
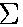 Fy =
- Mg - T2sin
Fy =
- Mg - T2sin +
T1sin
+
T1sin = May = 0
= May = 0
-
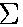 Fx =
T1cos
Fx =
T1cos +
T2cos
+
T2cos = Max =
= Max =
Mv2/R
- where we have used the fact that in circular motion a =
v2/R, and that there is no acceleration in the y-direction. Also, we have
- R = Lcos

- where L = the length of each string. Now, we have two equations (the y and
x equation above) in 2 unknowns (T1 and T2), assuming
we know the speed v. The speed v is known, since we have the rate of
revolution:
-
v = 2
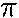 R/T
R/T
- = 2
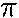 Lcos
Lcos /(1/3 s)
/(1/3 s)
- = 2
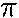 (0.6 m)cos30°/(1/3 s)
(0.6 m)cos30°/(1/3 s)
- = 9.79 m/s
- We can solve the equations for the tensions by rearranging:
- T1 + T2 = Mv2/Rcos

- from the x-equation and
- T1 - T2 = Mg/sin

- from the y-equation. Adding these two equations together gives us
T1, and subtracting them gives us T2:
- T1 = (M/2)[v2/Rcos
 + g/sin
+ g/sin ]
]
- T2 = (M/2)[v2/Rcos
 - g/sin
- g/sin ]
]
- Now plug in v=9.79 m/s, g=9.8 m/s2, R=Lcos
 =
(0.6m)cos30° = 0.52m, and M= 5 kg to these equations to get
=
(0.6m)cos30° = 0.52m, and M= 5 kg to these equations to get
- T1 = 582 N
- T2 = 484 N
- Note that T1 > T2 since the upper string is the one counteracting gravity
(through the vertical component of its tension).
Note: This was similar to problem 5-49 from the homework
(the only difference being that
we had two tensions instead of one normal force and one frictional force).
It is essentially the same as problem 5-60 from the text
(a level II problem).
Test 1 page
Physics 101 Home page
Physics Department Home Page
College of William and Mary,
Dept. of Physics
armd@physics.wm.edu
last updated: Oct. 5 2000
![]() = 30° .
If the system is rotated about the axis with frequency
of 3 revolutions per second, what are the tensions in the
two strings? (hint: they are not the same!)
= 30° .
If the system is rotated about the axis with frequency
of 3 revolutions per second, what are the tensions in the
two strings? (hint: they are not the same!) 