A pendulum consists of a bob of mass m attached to a weightless string of length L. The bob is pulled aside so that the string makes an angle with the vertical, and is released from rest. Find:

a) The speed v of the bob at the bottom of its swing.

b) The tension T in the string at that time.

a) We can apply conservation of energy. Choose the gravitational potential energy to be zero at the bottom of the swing. The initial energy is all potential, which is all converted to kinetic energy at the bottom of the swing. Thus

E_i = mgh = E_f = (1/2)mv²

But we are not given h, we are given L and the initial angle . The height h is given by (see figure)

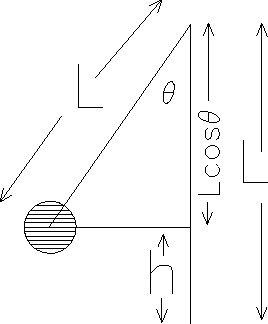
h = L - Lcos

= L(1-cos)

Thus we have

(1/2)mv² = mgL(1-cos)

v = [2gL(1-cos)]^1/2

b) Since we want tension, a force, we better do a force diagram for the bob when it is at the bottom of the swing, and apply F = ma. See figure:

T - mg = ma = mv²/L

where we have use the fact that the bob must have a centripetal acceleration, as it is going around a circle of radius L. Thus

T = mg + mv²/L = m(g + v²/L)

Note: This is problem 7-59 from the homework.

Next problem
Test 2 page
Physics 101 Home page
Physics Department Home Page