Problem 4:

A weight (m = 0.5 kg) on a string is swung in a vertical circle of radius R = 1.0 m, and undergoes uniform circular motion. The tension in the string is T = 4.0 N when the weight is at the top of the circle. What is the tension in the string when the weight is at the bottom of the circle?

Solution:

Uniform circular motion, so we have a = v²/r, directed towards center of circle.

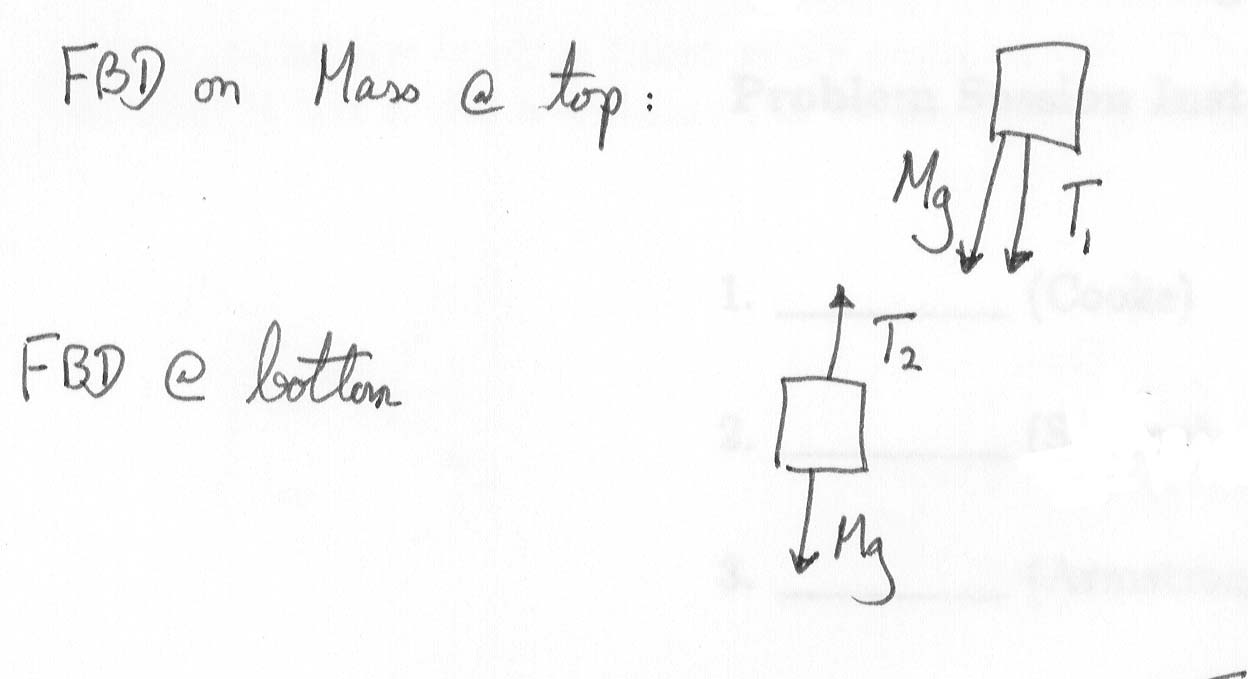
Draw a free-body diagram for the mass when it is at the top of the circle:

       F =  ma   =     T₁ + mg   =   mv²/r

where we are given that     T₁ = 4.0 N.

Now draw a free-body diagram for the mass when it is at the bottom (see above):

        F = ma =     T₂ - mg   =   mv²/r

Set the left-hand side of the two equations equal (since their right-hand sides are equal) and we get

        T₁ + mg = T₂ - mg

or

     T₂ = T₁ + 2mg   =    4.0 N + 2(0.5 kg)(9.8 m/s²)  =  13.8 N

(note: we didn't need to know the radius of the circle - that was a red herring...)

Test 2
Physics 101 Home page
Physics Department Home Page