Problem 4:

A constant force F = (3.0 N)i - (2.0 N)j is exerted on an object which moves from r1 = (1.0 m)i - (3.0 m)j to r2 = (4.0 m)i + (5.0 m) j.

What is the work done by this force on the object?

[bonus question (5 points) - do this part only if you have finished the rest of the test!] What is the angle between the vector F and the displacement vector?

Solution:

The work is the dot product (scalar product) of the force and the displacement.
W = F · 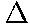r
The displacement is
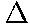r = r2 - r1
= [(4.0 m)i + (5.0 m) j] - [(1.0 m)i - (3.0 m)j]
= 3.0 m i + 8.0 m j
so
W = [(3.0 N) i - (2.0 N) j] · [3.0 m i + 8.0 m j]
= (3.0 N)(3.0 m) + (-2.0 N)(8.0 m) = -7 Nm = -7 J
The negative sign indicates that the force takes energy away from the object. Possibly other forces acted on the object during its motion...

Bonus: We can find the angle using the work we have just calculated, since W = Frcos. We find the magnitudes of the force and the displacement:
F = [(3.0 N)2 + (-2.0 N)2]1/2 = 3.61 N
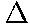r = [(3.0 m)2 + (8.0 m)2]1/2 = 8.54 m
Thus
cos = (-7 J)/[(3.61 N)(8.54 m)] = -0.2272
= 103.1°

Note:

This was essentially the same as 6-20 from the homework. The bonus portion was done as an example in the lecture.

Test 2 page
Physics 101 Home page
Physics Department Home Page

College of William and Mary,
Dept. of Physics
armd@physics.wm.edu
last updated: Oct. 20 2000