A block (m₁ = 1.5 kg) rests on top of another block (m₂ = 2.0 kg), which rests on a frictionless level surface. The coefficient of static friction between the two blocks is µ_s = 0.3.

  a) What is the maximum horizontal force that can be applied to the upper block such that the blocks move together, without the upper one sliding on the lower one?
  b) Repeat, this time for a horizontal force applied to the lower block.

Solution:

a) The method of solution always starts the same for a problem like this: draw the force diagrams, and apply F = ma. Consider the force diagram for each mass individually:

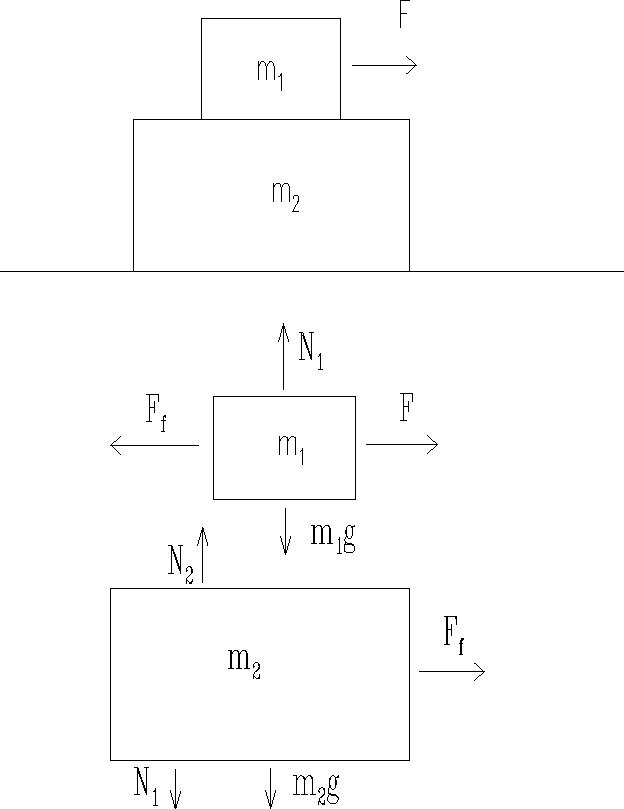
For the lower mass, there is only one force in the x-direction, which is the friction from the upper mass:

1) F_2x = F_f = m₂a

For the upper mass, the horizontal forces are the external force and the frictional force from the lower mass:

2) F_1x = F - F_f = m₁a

Notice that we have used Newton's third law to tell us that the frictional force exerted by m₁ on m₂ (i.e. the only horizontal force on m₂) is equal and opposite to the frictional force on m₁. Notice also that we have used the fact the two masses are accelerating together, i.e. the a's are the same in both equations.

Now, we use the force in the y-direction (where the acceleration is zero) for the upper mass to get

F_1y = N₁ - m₁g = 0

thus

N₁ = m₁g

Since we want the maximum force, we should use the maximum frictional force, so we have

F_f = µ_sN₁

which gives

3) F_f = µ_s m₁g

Now we can combine Eqs. 1) and 3) to get

µ_s m₁g = m₂a

or

a = µ_s m₁g/m₂

Now, add equations 1) and 2), and then substitute in the relation for a:

F = (m₁ + m₂)a

F = (m₁ + m₂)µ_s m₁g/m₂

Substituting in numbers we get

F = (1.5 kg + 2.0 kg)0.30(9.8 m/s²)(1.5 kg)/(2.0 kg)

= 7.7 N

b) The force diagrams and equations are almost the same as above, except force F now acts only on the lower block, and so we have

1) F_f = m₁a

2) F-F_f = m₂a

3) F_f = µ_sm₁g

so we combine 1) and 3) to give

a = µ_sg

and, again adding 1) and 2) and sticking in the above relation for   a   we get

F = (m₁ + m₂)µ_sg

= (1.5 kg + 2.0 kg)0.30(9.8 m/s²)

= 10.3 N

Note: This was identical to problem 5-32

Next problem
Test 1 page
Physics 101 Home page
Physics Department Home Page