Problem 1:

A coin of mass = 4 g lies on a copy of Tipler's physics textbook, which is being tilted at an angle with respect to the horizontal. The coefficient of static friction between the coin and the book is _s = 0.4 and the coefficient of kinetic friction is _k = 0.3.

a) Find the maximum angle at which the book can be tilted before the coin will start to slide.

b) Assume the book is tilted at an angle of 60°. What will be the kinetic energy of the coin after it has a slid a distance l = 15 cm along the cover of the book?

Solution:

Draw a Free-body diagram for the coin:

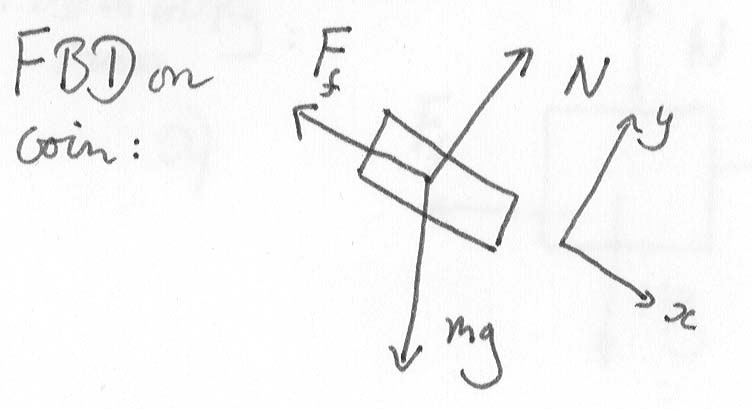
Apply F = m a to the coin, and we get:

       (x)    mgsin - F_f = ma_x   =  0    (the coin does not slide) 

       (y)    N - mgcos = 0     (no acceleration in y-direction)

We also have

      F_{f  s} N

The maximum angle before sliding will be when the frictional force is at its maximum, so we have

       F_f  =  _s N    = _s mgcos  

Thus we have from the x-equation

         mgsin - _s mgcos =  0

thus

      _s  = sin/cos = tan

       = arctan(_s ) = 21.8°

b) The change in kinetic energy is the work done by the net force; the net force acting on the coin is

        F = mgsin - _k mgcos

where we use kinetic friction, since coin is sliding. The work done is

     W = Fx = F l = (mgsin - _k mgcos)l  =  4.21 x 10^-3 J

Alternate solution : We can calculate the acceleration using a = F/m where F is as above, then use

      v_f² = v₀² + 2 ax

to solve for the final velocity v_f   and then calculate the kinetic energy as ½ mv²

Problem 2
Test 2
Physics 101 Home page
Physics Department Home Page