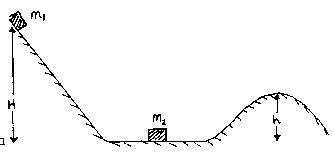A roller coaster car of mass m₁ = 100 kg starts rolling from rest at the top of a track at a height H = 50 m. At the bottom of the hill, it collides with another car of mass m₂ = 100 kg which is initially at rest. The two cars stick together and head for a second hill of height h = 10 m.

a) What is the speed of the first car just before the collision?

b) What is the speed of the two combined cars just after the collision?

c) Show whether or not they will make it to the top of the second hill.

d) If the collision occurs in t = 0.1 s, what is the average force exerted on the second car during the collision?

a) Energy is conserved during the roll down the hill:

E_initial = m₁gH   =   E_final = (1/2)m₁v₁²

thus

v₁ = [2gH]^1/2

= [2(9.8 m/s²)(50 m)]^1/2 = 31.3 m/s

b) Now momentum (but not energy) is conserved during the collision of the cars; this is just a one-dimensional perfectly inelastic collision, so we have

p_initial = m₁v₁ + 0   =   p_final = (m₁ + m₂)v

v = [m₁/(m₁ + m₂)]v₁

= [100 kg/(100 kg + 100 kg)](31.3 m/s) = 15.65 m/s

c) If the combined cars are to make it to the top of the hill, their initial kinetic energy must exceed their potential energy at the hill's top (so that their kinetic energy at the top is > zero). Their initial kinetic energy is

K = (1/2)(m₁ + m₂)v²

= (1/2)(200 kg)(15.65 m/s)² = 24.5 x 10³ J

Their potential energy at the top of the second hill is

U = (m₁ + m₂)gh

= (200 kg)(9.8 m/s²)(10 m) = 19.6 x 10³ J

Thus K > U, so, yes, they will make it over the hill (with energy to spare).

d) The impulse J is given by

J = 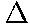p = F_average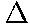t

We are interested in the average force exerted on the 2^nd car, so we need to consider the change in its momentum due to the collision; its initial momentum is zero, so its momentum change is just its final momentum which is

p₂^final = m₂v

thus the average force is

F_average = m₂v/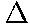t

= (100 kg)(15.65 m/s)/(0.1 s) = 1.56 x 10⁴N

The direction of this force is in the direction of p₂^final, i.e. to the right on the figure. As an aside, one could also have calculated the momentum change of the first car to get the average force exerted on it, and one would then get an equal (but opposite in direction) result (the 3^rd law!).

Next problem
Test 2 page
Physics 101 Home page
Physics Department Home Page